Customer Segmetation
고객 세분화는 조직의 고객 기반을 다양한 고객 속성에 따라 여러 섹션 또는 세그먼트로 나누는 프로세스와 유사하다. 고객 세분화 프로세스는 고객의 행동과 패턴 간의 차이를 찾는 전제를 기반으로 하게된다.
이에 따른 고객 세분화 동기의 주요 목표와 이점은 다음과 같다.
- Higher Revenue : 모든 고객 세분화 프로젝트에서 가장 분명한 요구 사항이자 모든 기업의 궁극적인 목표라고 할 수있다.
- Customer Understanding : 가장 폭넓게 수용되는 비즈니스 패러다임 중 하나는 "고객 파악" 이며 고객들을 세분화하면 이러한 패러다임을 완벽하게 분석 할 수 있다.
- Target Marketing : 고객 세분화의 가장 주요한 전략은 마케팅 활동에 효과적이고 효율적으로 집중할 수 있다는 것이다. 기업이 고객 기반의 다양한 세그먼트를 알고 있다면 해당 세그먼트에 적합한, 특화된 차별적인 마케팅 캠페인을 고안 할 수 있다. 이로써 고객 요구 사항을 더 잘 이해할 수 있으므로 조직에서의 마케팅 캠페인의 성공 가능성이 높아진다.
- Optimal Product Placement : 우수한 고객 세분화 전략은 기업이 새로운 제품을 개발 또는 제공하거나, 일부제품들을 결합된 제품으로 함께 제공하는 데 도움이 된다.
- Finding Latent Customer Segments : 마케팅 캠페인 또는 새로운 비즈니스 개발에 중점을 두는 과정에서 잠재적 고객들을 식별하는 것에 기여하고 놓칠 수 있는 세분화된 디테일에 주목한다.
Aim
소비자들의 구매에 대한 로그 데이터를 활용하여 유사한 특성을 가진 집단들을 파악하여 나눈다. 해당 분석에서는 RFM Model을 기반으로, 비지도학습 방법인 Clustering을 사용해 고객들을 분류한다. 일정 수의 집단으로 분류된 고객 집단들을 통해 집단을 대표하는 특성을 파악하고 집단별로 추측되는 성향을 정리한다. 이는 곧 기업 내부의 차별화된 마케팅 방안으로 유도될 수 있고 하나의 제언으로 작용할 수 있다.
Data description
사용하는 데이터는 총 (541909, 8) shape의 정형 데이터로써 온라인 Commercial에 대한 고객들의 구매 데이터이다. 각 행은 상품에 대한 한건의 구매를 나타내게된다.
Column description
총 8개의 변수로 구성된다.
- InvoiceNo: A unique identifier for the invoice. An invoice number shared across rows means that those transactions were performed in a single invoice (multiple purchases).
- StockCode: Identifier for items contained in an invoice.
- Description: Textual description of each of the stock item.
- Quantity: The quantity of the item purchased.
- InvoiceDate: Date of purchase.
- UnitPrice: Value of each item.
- CustomerID: Identifier for customer making the purchase.
- Country: Country of customer.
※ 여기서 주의할점은 한행은 언급했듯이 한건의 구매내역을 나타낸다. 그렇기에 한 고객이 다양한 상품들을 동시에 주문한 경우 InvoiceNo는 해당건들에 대해서 동일한 값을 가진다. 따라서 해당 컬럼을 통해 고객이 동시에 구매했는지 다른시점에 각각 구매했는지 여부를 판단할 수 있다.
1. Load Datasets and Setting
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib as mpl
import matplotlib.mlab as mlab
import matplotlib.cm as cm
import warnings
warnings.filterwarnings('ignore')
#그래프 시각화 옵션 설정함수
%matplotlib inline
sns.set(style="ticks", color_codes=True, font_scale=1.2)
color = sns.color_palette()
sns.set_style('darkgrid')
#그래프의 한글을 더욱 선명하게 출력
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('retina')
#그래프에서 음수 값이 나올 때, 깨지는 현상 방지
mpl.rc('axes',unicode_minus=False)data=pd.read_excel('Online Retail.xlsx')
data.head()
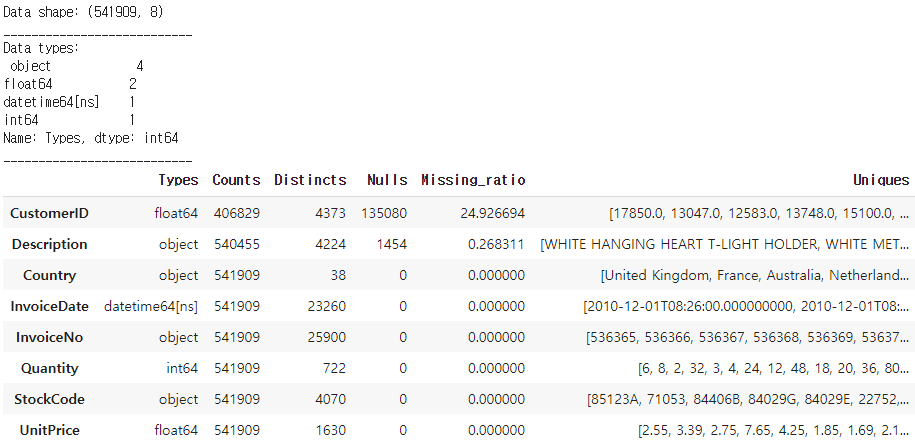
# 데이터의 관측치, 컬럼유형, 결측률 등의 일반적인 정보를 정리함
def str_summary(df, pred=None):
obs = df.shape[0]
types = df.dtypes
counts = df.apply(lambda x: x.count())
uniques = df.apply(lambda x: [x.unique()]).T.squeeze()
nulls = df.apply(lambda x: x.isnull().sum())
distincts = df.apply(lambda x: x.unique().shape[0])
missing_ratio = (df.isnull().sum()/ obs) * 100
print('Data shape:', df.shape)
cols = ['Types', 'Counts', 'Distincts', 'Nulls', 'Missing_ratio', 'Uniques']
structure = pd.concat([types, counts, distincts, nulls, missing_ratio, uniques], axis = 1, sort=True)
structure.columns = cols
print('___________________________\nData types:\n',structure.Types.value_counts())
print('___________________________')
return structure
data_summary = str_summary(data)
display(data_summary.sort_values(by='Missing_ratio', ascending=False))사용될 데이터가 가진 정보들을 한번에 볼 수 있는 str_summary 함수로 6가지 정보들을 table형태로 파악할 수 있다.
보통 파이썬에서는 info() 함수를 사용해 간단하게 파악하지만 해당 함수를 사용해 자세한 정보들을 더 정리된 형태로 파악한다.
2. Pre-Processing
해당 데이터는 소비자가 구매한 경우 발생되는 구매내역에 대한 로그데이터이다. 해당단계에서는 발생하는 이상치 또는 결측치들을 처리하고 향후 분석 또는 시각화가 편리할 형태로 정제하는 과정을 거친다.
- Case 1: Quantity & UnitPrice <= 0
# 수량과 개별단가가 0 미만이 존재하는 경우
print('Check if we had negative quantity and prices at same register:','No'
if data[(data.Quantity<0) & (data.UnitPrice<0)].shape[0] == 0 else 'Yes', '\n')
# 수량과 개별단가가 0 이하가 존재하는 경우의 수
print('Check how many register we have where quantity is negative', 'and prices is 0 or vice-versa:',
data[(data.Quantity<=0) & (data.UnitPrice<=0)].shape[0],'\n')
# 수량과 개별단가가 0 이하가 존재하는 경우의 CustomerID의 고유값
print('What is the customer ID of the registers above:',
data.loc[(data.Quantity<=0) & (data.UnitPrice<=0),['CustomerID']].CustomerID.unique(),'\n')
# 전체 데이터 중 수량과 개별 단가가 0 이하의 값을 갖는 경우
data.loc[(data.Quantity<=0) & (data.UnitPrice<=0)]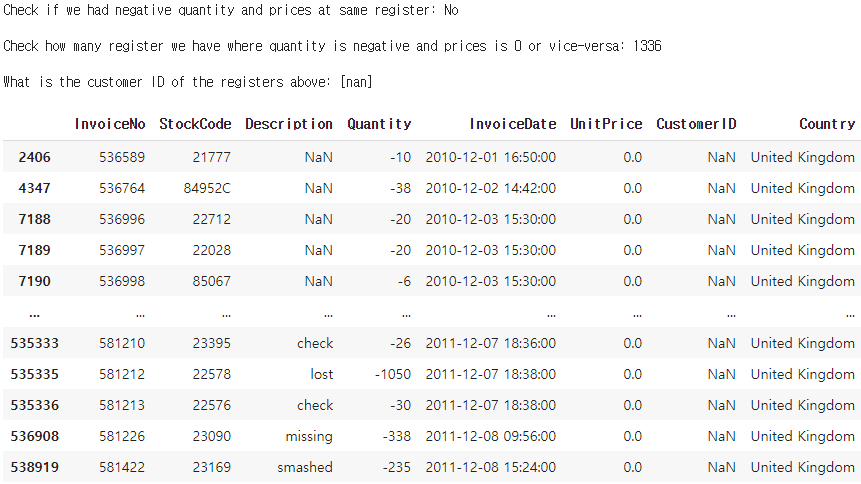
약 1336건이 개별단가와 수량에 있어서 0이하의 값을 가진다. 해당 경우에는 CustomerID가 한건도 존재하지않는다.
- Case 2: Quantity < 0
# 전체 데이터 중 수량이 0 미만의 값을 갖는 비율
print('% Negative Quantity: {:.2%}\n'.format(data[(data.Quantity<0)].shape[0]/data.shape[0]))
# 음의 수량을 갖는 경우의 InvoiceNo는 모두 'C' 라는 값으로 시작함
# 음의 수량을 갖는 경우는 환불의 경우라고 추측해볼 수 있음
print('All register with negative quantity has Invoice start with:',
data.loc[(data.Quantity<0) & ~(data.CustomerID.isnull()), 'InvoiceNo'].apply(lambda x: x[0]).unique(),'\n')
data.loc[(data.Quantity<0) & ~(data.CustomerID.isnull())]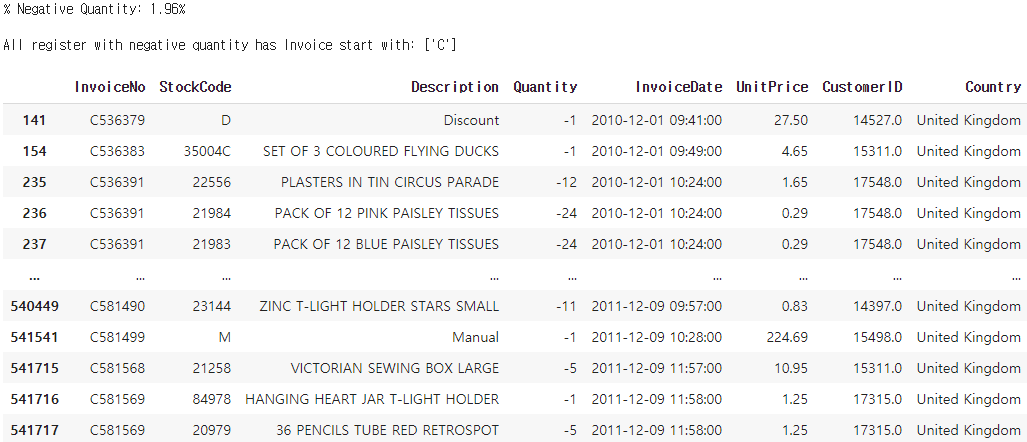
전체 관측치 중 수량이 0미만의 값을 같는 비율은 1.96%로 8905건이 집계되었다. 또한 해당 경우는 CustomerID가 존재하는 경우와 존재하지 않는 경우를 모두 포함하고있는데, 존재하는 경우에는 InvoiceNo는 앞글자가 모두 'C' 로 시작한다. 현재 데이터에 대한 추가적인 정보는 명시되어있지 않아 이것이 무엇을 의미하는지 확신할 수는 없으나, 두가지로 유추해볼 수 있다.
C는 Cancel의 약자로 주문을 취소한 경우를 나타내거나, 혹은 환불한 경우를 나타내는 것일 수 있다. 추가적으로 CustomerID가 Null인 경우는 재고정리나 주문, 배송 누락등으로 음수의 수량을 갖게된 경우를 의미하는 것으로도 해석할 수있다. 이를 통해 환불 또는 반품건에 대한 추가적인 분석이나, 불만 여부에 대해 예측하는 분석이 이뤄질 수 있으나 여기서는 기존 목적에 집중한다.
- Case 3: UnitPrice < 0
# 개별단가가 0 미만인 경우
print('Negative UnitPrice:\n')
display(data[(data.UnitPrice<0)])
# 개별단가가 0일때 고객ID가 존재하는 경우: 40건으로 집계
print("\nSales records with Customer ID and zero in Unit Price:",data[(data.UnitPrice==0) & ~(data.CustomerID.isnull())].shape[0],'\n')
data[(data.UnitPrice==0) & ~(data.CustomerID.isnull())]
개별단가가 0 미만인 경우는 총 2건이며 CustomerID는 존재하지않는다. 해당 품목은 'Adjust bad debt' 로 불량 부채조정을 의미한다. 해당 건은 상품에 대한 구매라고 보기어려우며 기업내부의 정책적인 조정에 의해 지출된 금액으로 파악된다. Price역시 타상품들에 비해 월등히 높은 값을 가진다. 소비자들의 구매가 주를 이루는 데이터에서 해당 두 행은 적합하지 않은 것으로 판단되며 추후 제거가 필요하다. 다음으로 개별단가가 0미만 일때 고객 ID가 존재하는 경우는 40건으로 집계 되었다.
# 고객 ID가 존재하지 않는 경우 제거
data = data[~data.CustomerID.isnull()]
# 고객 ID를 정수형으로 변경
data['CustomerID'] = data['CustomerID'].astype(int)
# 수량은 0 이상, 개별단가는 0 초과인 경우만 집계
data = data[data.Quantity>=0]
data = data[data.UnitPrice>0]
str_summary(data)
CustomerID를 기반으로 Clustering이 이루어지게된다. 따라서 결측치와 조건에 부합하지 않는 데이터들을 제거한다. 이렇게 정제된 데이터는 총 397884건의 로그를 가지며 모든 행의 결측치는 사라졌다.
# 수량과 개별단가를 곱하여 Monetary라는 매출 파생변수를 생성
data['Monetary'] = data.Quantity*data.UnitPrice
data=data.reset_index(drop=True)마지막으로 EDA에서 주요하게 사용될 매출에 관한 컬럼인 'Monetary' 컬럼을 생성한다. 이로써 1차적인 전처리는 완료되었으며, 정제된 데이터를 바탕으로 EDA를 진행하고 주요 고객과, 상품, 판매처등을 보여준다.
3. Exploratory Data Analysis Via Visualization
3.1 지역별 매출액 분포
# 국가별로 대륙을 분리
europe=['United Kingdom', 'Germany', 'France', 'EIRE', 'Spain', 'Netherlands',
'Belgium', 'Switzerland', 'Portugal', 'Australia', 'Norway', 'Italy',
'Channel Islands', 'Finland', 'Cyprus', 'Sweden', 'Austria', 'Denmark',
'Poland','Iceland','Greece','Malta','European Community','Lithuania', 'Czech Republic']
asia=['Japan','Singapore','Australia']
america=['USA','Canada','Brazil']
elses=['Israel','RSA','Lebanon','United Arab Emirates','Saudi Arabia','Bahrain','Unspecified']
# 대륙별 매핑한 새로운 컬럼을 생성
data['Continent']=0
data['Continent'][data[data['Country'].isin(europe)].index]='Europe'
data['Continent'][data[data['Country'].isin(asia)].index]='Asia'
data['Continent'][data[data['Country'].isin(america)].index]='America'
data['Continent'][data[data['Country'].isin(elses)].index]='else'# 대륙별, 국가별 1인당 평균 매출액을 계산하여 시각화함
fig = plt.figure(figsize=(25, 6))
f1 = fig.add_subplot(121)
country_sales = data.groupby(['Country'])['Monetary'].mean().sort_values(ascending = False).plot(kind='bar', title='Average Sales by Country',color=plt.cm.Paired(np.arange(10)))
f2 = fig.add_subplot(122)
cont = data.groupby(['Continent']).Monetary.mean().sort_values(ascending = False)
continents_sales = plt.pie(cont, labels=cont.index, autopct='%1.1f%%', shadow=True, startangle=90)
plt.title('Average Sales of Continents')
plt.show()

국가를 기반으로 국가별, 대륙별 1인당 평균 매출액을 집계했다. Netherlands, Austrailia, Japan 등이 타 국가에 비해 상대적으로 매우 높은 수치를 갖는다. 대륙 별로 평균매출액에 있어서의 기여도는 Asia, America, Europe 순으로 높게 나타났다.
3.2 금액, 빈도별 상위 고객 분포
# 고객별 매출액의 합계, 구매횟수의 합계를 계산함
top_sales_sum=data.groupby(["CustomerID"]).Monetary.sum().sort_values(ascending = False) # 고객별 매출액의 합계를 계산함
top_sales_cnt=data.groupby(["CustomerID"]).Monetary.count().sort_values(ascending = False) # 고객별 구매횟수의 합계를 계산함
# 상위 n명 고객들의 매출 비율, 구매횟수 비율을 계산
top_sales_percent_40 = np.round((top_sales_sum.head(40).sum()/top_sales_sum.sum()) * 100, 2)
top_sales_percent_10_sum = np.round((top_sales_sum.head(10).sum()/top_sales_sum.sum()) * 100, 2)
top_sales_percent_10_cnt = np.round((top_sales_cnt.head(10).sum()/top_sales_cnt.sum()) * 100, 2)
fig = plt.figure(figsize=(20, 6))
top40 = top_sales_sum.head(40).plot(kind='bar', title='Top Customers: {:.2f}% Sales'.format(top_sales_percent_40),color=plt.cm.Paired(np.arange(10)))
fig = plt.figure(figsize=(20, 6))
f1 = fig.add_subplot(121)
top10_sales = top_sales_sum.head(10).plot(kind='bar', title='Top 10 Customers: {:.2f}% Sales'.format(top_sales_percent_10_sum),color=plt.cm.Set3(np.arange(10)))
f1 = fig.add_subplot(122)
top10_event = top_sales_cnt.head(10).plot(kind='bar', title='Top 10 Customers: {:.2f}% Event Sales'.format(top_sales_percent_10_cnt),color=plt.cm.Set3(np.arange(10)))
첫번째 Plot은 매출 기준 상위 40명의 Sales를 나타내며 하단의 두가지는 각각 매출과 구매횟수(구매상품수)의 상위 10명의 분포를 보여준다. Sales에 있어서 상위 10명의 고객들은 전체 매출의 17.26%를 차지하며, Events에 있어서 상위 10명은 전체 구매횟수에 8.93%를 차지한다. 해당 데이터에서는 상품종류를 다양하게 구매한 고객 보다는 구입수량이 많거나 고가의 상품을 구매한 고객들이 매출의 큰 비중을 차지하고 있는 것으로 보여진다.
3.3 금액, 빈도별 상위 품목 분포
# 품목별 판매금액의 합계 테이블(Monetary_sum)과 품목별 판매빈도 테이블(inv_nunique)을 생성
Monetary_sum = data.groupby(["Description"]).Monetary.sum().sort_values(ascending = False)
inv_nunique = data.groupby(["Description"]).InvoiceNo.nunique().sort_values(ascending = False)
# 판매 금액을 기준으로 상위 10개 품목에 대한 매출 그래프
fig = plt.figure(figsize=(18, 6))
f1 = fig.add_subplot(121)
Top10 = list(Monetary_sum[:10].index)
PercentSales = np.round((Monetary_sum[Top10].sum()/Monetary_sum.sum()) * 100, 2)
PercentEvents = np.round((inv_nunique[Top10].sum()/inv_nunique.sum()) * 100, 2)
g = Monetary_sum[Top10].plot(kind='bar',color=plt.cm.Paired(np.arange(10)))
plt.title('Top 10 Products in Sales: {:.2f}% of Monetary and {:.2f}% of Events'.format(PercentSales, PercentEvents))
# 판매 횟수를 기준으로 상위 10개 품목에 대한 횟수 그래프
f1 = fig.add_subplot(122)
Top10Ev = list(inv_nunique[:10].index)
PercentSales = np.round((Monetary_sum[Top10Ev].sum()/Monetary_sum.sum()) * 100, 2)
PercentEvents = np.round((inv_nunique[Top10Ev].sum()/inv_nunique.sum()) * 100, 2)
g = inv_nunique[Top10Ev].plot(kind='bar',color=plt.cm.Paired(np.arange(10)))
plt.title('Events of top 10 most sold products: {:.2f}% of Monetary and {:.2f}% of Events'.format(PercentSales, PercentEvents))
왼쪽은 매출기준의 상위 10개 품목이며 전체 매출의 약 10%, 구매되는 빈도에 있어서 약 3%를 차지한다. 우측은 구매횟수 기준의 상위 10개 품목이며 전체 매출의 약 7%, 구매 빈도에 있어서는 약 3.5%를 차지한다.
주목할점은, WHTE HANGING HEART T-LIGHT HOLDER, JUMBO BAD RED RETROSPOT, REGENCY CA KESTAND 3TIER등의 제품은 두 그래프에 모두 등장한다. 즉 매출에 대한 기여도도 높으며 동시에 소비자들의 구매빈도역시 높은 주요한 상품이라고 할 수있다.
# 판매 빈도 기준 상위 20개 상품의 매출금액 분포
fig = plt.figure(figsize=(15, 6))
Top20ev = list(inv_nunique[:20].index)
PercentSales = np.round((Monetary_sum[Top20ev].sum()/Monetary_sum.sum()) * 100, 2)
PercentEvents = np.round((inv_nunique[Top20ev].sum()/inv_nunique.sum()) * 100, 2)
g = Monetary_sum[Top20ev].sort_values(ascending = False).plot(kind='bar',
title='Sales of top 20 most sold products: {:.2f}% of Monetary and {:.2f}% of Events'.format(PercentSales, PercentEvents),
color=plt.cm.Paired(np.arange(10)))
# 판매 금액 기준 상위 20개 상품의 판매빈도 분포
fig = plt.figure(figsize=(15, 6))
Top20 = list(Monetary_sum[:20].index)
PercentSales = np.round((Monetary_sum[Top20].sum()/Monetary_sum.sum()) * 100, 2)
PercentEvents = np.round((inv_nunique[Top20].sum()/inv_nunique.sum()) * 100, 2)
g = inv_nunique[Top20].plot(kind='bar', title='Top 20 most sold products: {:.2f}% of Monetary and {:.2f}% of Events'.format(PercentSales, PercentEvents),
color=plt.cm.Paired(np.arange(10)))
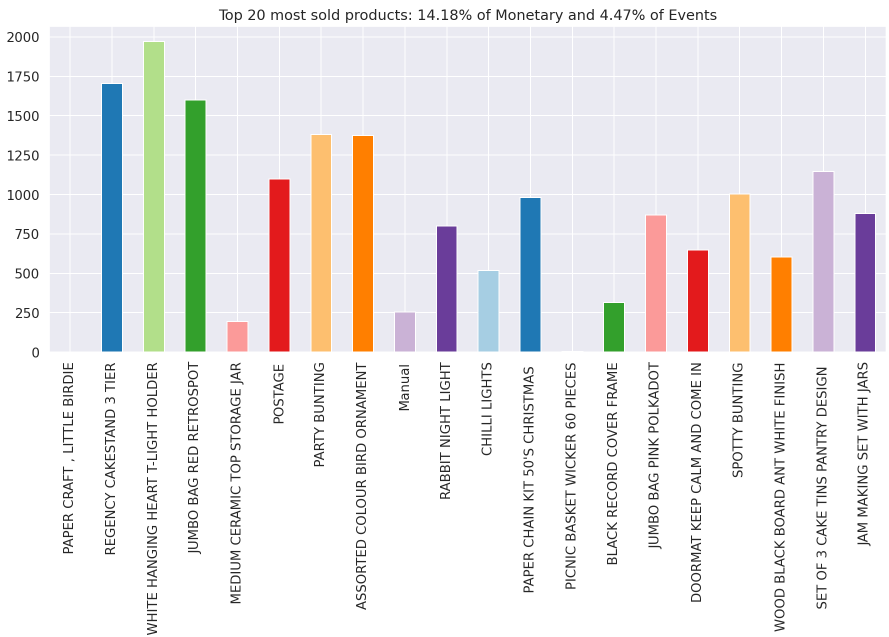
마지막으로 상품별 매출과 구매빈도의 관점에서 상품들을 비교한다. 판매빈도 기준 20개의 상품의 매출들을 보면 대체로 판매빈도가 높을수록 매출금액이 높게 나타난다. 하지만 판매금액에서 바라보면 큰 차이가 나타나는데, 매출치가 높다고해서 소비자들이 반드시 많이 구매하는 상품은 아니며, 극단적으로 PAPER CRAFT, LITTLE BIRDIE와 같은 경우는 구매 빈도가 100건도 채 되지않으나 높은 상품 금액으로인해 매출의 가장 큰 비중을 차지하고있다. 이러한 구매빈도와 매출금액의 괴리는 상품별로 자세히 고려해볼 여지를 남긴다.
4. Clustering For Customer Segmentation
4.1 RFM Model

분석의 기반이되는 RFM 모델은 고객들의 거래 및 정보에서 중요한 가치인 3가지를 고려하는데 각각 Recency, Frequency, Monetary 이다.
- Recency: 특정 시점을 기준으로 고객의 구매의 최근성
- Frequency: 고객이 거래를 실행한 빈도
- Monetary: 고객의 거래에 의해 발생한 수익 및 매출의 총체
import datetime
from scipy import stats
from scipy.stats import skew, norm, probplot, boxcox, kurt
from sklearn.preprocessing import StandardScaler
import mathdef QQ_plot(data, measure):
fig = plt.figure(figsize=(20,7))
#Get the fitted parameters used by the function
(mu, sigma) = norm.fit(data)
#Kernel Density plot
fig1 = fig.add_subplot(121)
sns.distplot(data, fit=norm)
fig1.set_title(measure + ' Distribution ( mu = {:.2f} and sigma = {:.2f} )'.format(mu, sigma), loc='center')
fig1.set_xlabel(measure)
fig1.set_ylabel('Frequency')
#QQ plot
fig2 = fig.add_subplot(122)
res = probplot(data, plot=fig2)
fig2.set_title(measure + ' Probability Plot (skewness: {:.6f} and kurtosis: {:.6f} )'.format(data.skew(), data.kurt()), loc='center')
plt.tight_layout()
plt.show()# 기준날짜를 지정
refrence_date = data.InvoiceDate.max() + datetime.timedelta(days = 1)
print('Reference Date:', refrence_date)
data['Recency'] = (refrence_date - data.InvoiceDate).astype('timedelta64[D]')
# 기준 날짜로부터 고객의 최종 접속일이 며칠이 떨어져있는지를 계산
rfm = data[['CustomerID', 'Recency']].groupby("CustomerID").min().reset_index()
# Density plot과 qqplot을 통해 분포와 정규성 여부를 판단
QQ_plot(rfm.Recency, 'Recency')

거래의 최종 날짜에 하루를 더하여 Recency를 측정할 기준날짜를 지정하고, 기준날짜로부터 고객의 최종 접속일이 얼마나 떨어져있는지를 고객별로 계산한다. Recency 변수를 생성하고 분포를 확인한 결과, 주로 좌측으로 skew된 편향된 분포를 가지며 정규성을 만족하지 않는 모습을 보여준다.
# 같은 접속에서 구매한 경우, frequency를 측정시 중복됨
# 이에 따른 중복을 제거하고 고객별 방문빈도를 측정
freq = data[['CustomerID', 'InvoiceNo']].drop_duplicates().groupby('CustomerID').count().reset_index()
freq.columns=['CustomerID', 'Frequency']
rfm=pd.merge(rfm,freq,how='left')
QQ_plot(rfm.Frequency, 'Frequency')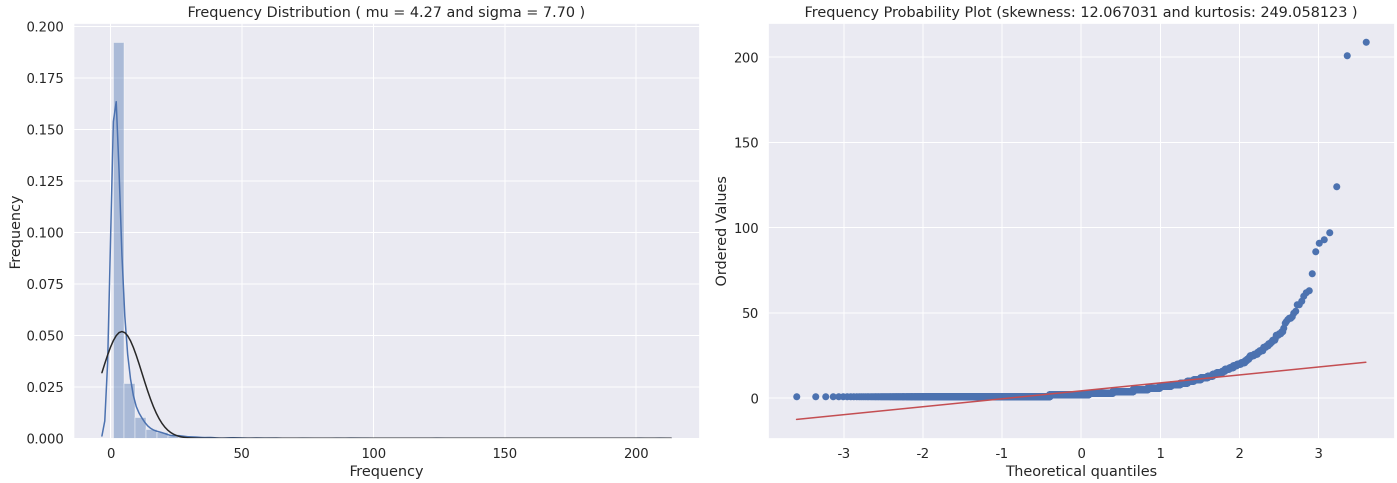
# 고객별 매출의 합계를 측정
Monetary = data[['CustomerID', 'Monetary']].groupby("CustomerID").sum().reset_index()
rfm = rfm.merge(Monetary)
QQ_plot(rfm.Monetary, 'Monetary')
Frequency, Monetary에 대해서도 RFM 모델의 논리에 따라 CustomerID별로 수치를 집계하고, 분포를 파악한다.
R, F, M 모두가 좌측으로 편향된 분포를 가지는 것을 확인할 수 있으며 분산이 지나치게 큰 값을 보이는 경우가 많아 추후 정규화가 필요하다.
# R, F, M 컬럼의 정규화를 위해 각각 log를 취함
rfm['Recency_log'] = rfm['Recency'].apply(math.log)
rfm['Frequency_log'] = rfm['Frequency'].apply(math.log)
rfm['Monetary_log'] = rfm['Monetary'].apply(math.log)
features = ['Monetary_log', 'Recency_log','Frequency_log']
X_subset = rfm[features]
# 컬럼별로 정규화를 실행
st = StandardScaler().fit(X_subset)
X_scaled = st.transform(X_subset)
rfm_log=pd.DataFrame(X_scaled, columns=X_subset.columns)Log - Transformation을 통해 분산을 안정화시켜주는 정규화를 진행하고, 마지막으로 StandardSclaer로 평균이 0, 분산이 1을 가지는 분포로 생성함으로써 Clustering을 위한 전처리는 끝나게된다.
4.1 K-Mean Clustering
def visualize_kmeans(cluster_list,feature_columns,X):
cluster_centers = dict()
for n_clusters in cluster_list:
fig, (ax1, ax2, ax3) = plt.subplots(1, 3)
fig.set_size_inches(20, 6)
ax1.set_xlim([-0.1, 1])
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
clusterer = KMeans(n_clusters=n_clusters, init='k-means++', n_init=10,max_iter=300, tol=1e-04, random_state=123)
cluster_labels = clusterer.fit_predict(X)
silhouette_avg = silhouette_score(X = X, labels = cluster_labels)
cluster_centers.update({n_clusters :{'cluster_center':clusterer.cluster_centers_,
'silhouette_score':silhouette_avg,
'labels':cluster_labels}
})
sample_silhouette_values = silhouette_samples(X = X, labels = cluster_labels)
y_lower = 10
for i in range(n_clusters):
ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.Spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
ax1.set_title("The silhouette plot for the various clusters")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([])
ax1.set_xticks([-0.1, 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1])
colors = cm.Spectral(cluster_labels.astype(float) / n_clusters)
centers = clusterer.cluster_centers_
y = 0
x = 1
ax2.scatter(X[:, x], X[:, y], marker='.', s=30, lw=0, alpha=0.7, c=colors, edgecolor='k')
ax2.scatter(centers[:, x], centers[:, y], marker='o', c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax2.scatter(c[x], c[y], marker='$%d$' % i, alpha=1, s=50, edgecolor='k')
ax2.set_title("{} Clustered data".format(n_clusters))
ax2.set_xlabel(features[x])
ax2.set_ylabel(features[y])
x = 2
ax3.scatter(X[:, x], X[:, y], marker='.', s=30, lw=0, alpha=0.7, c=colors, edgecolor='k')
ax3.scatter(centers[:, x], centers[:, y], marker='o', c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax3.scatter(c[x], c[y], marker='$%d$' % i, alpha=1, s=50, edgecolor='k')
ax3.set_title("Silhouette score: {:1.2f}".format(cluster_centers[n_clusters]['silhouette_score']))
ax3.set_xlabel(features[x])
ax3.set_ylabel(features[y])
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()
return cluster_centers# K = 3, 4, 5 일때 결과를 시각화하고 이때 cluster별 중심을 저장
cluster_centers=visualize_kmeans([3,4,5],features,X_scaled)
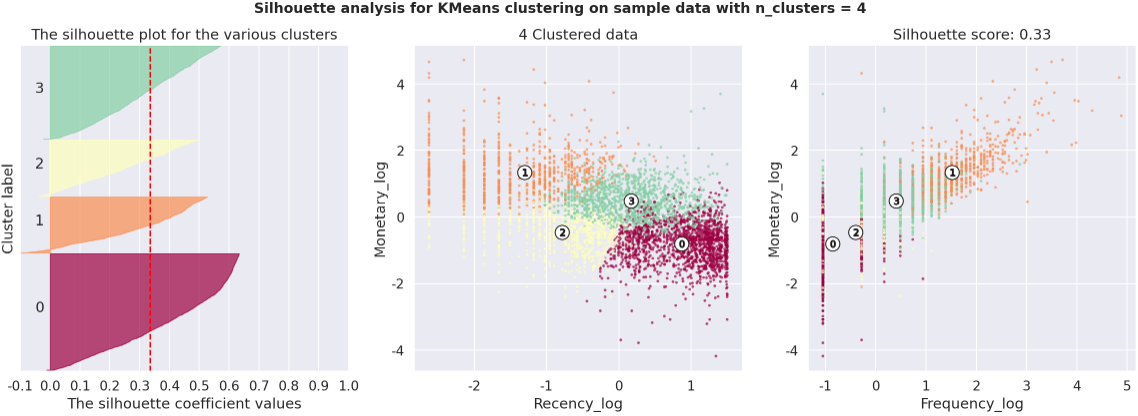

K-Means Clustering은 사전에 K의 값을 지정해주는 것이 필요하며, 각각 3. 4. 5 로 지정하여 비교했다. 군집분석은 비지도학습으로써 객관적으로 정의된 평가 지표는 없으나, Dunn Index, Silhouette Score등으로 군집분석의 타당성을 유추할 수 있다. 해당 분석에서는 Silhouette Score를 사용했다. 식은 다음과 같다.

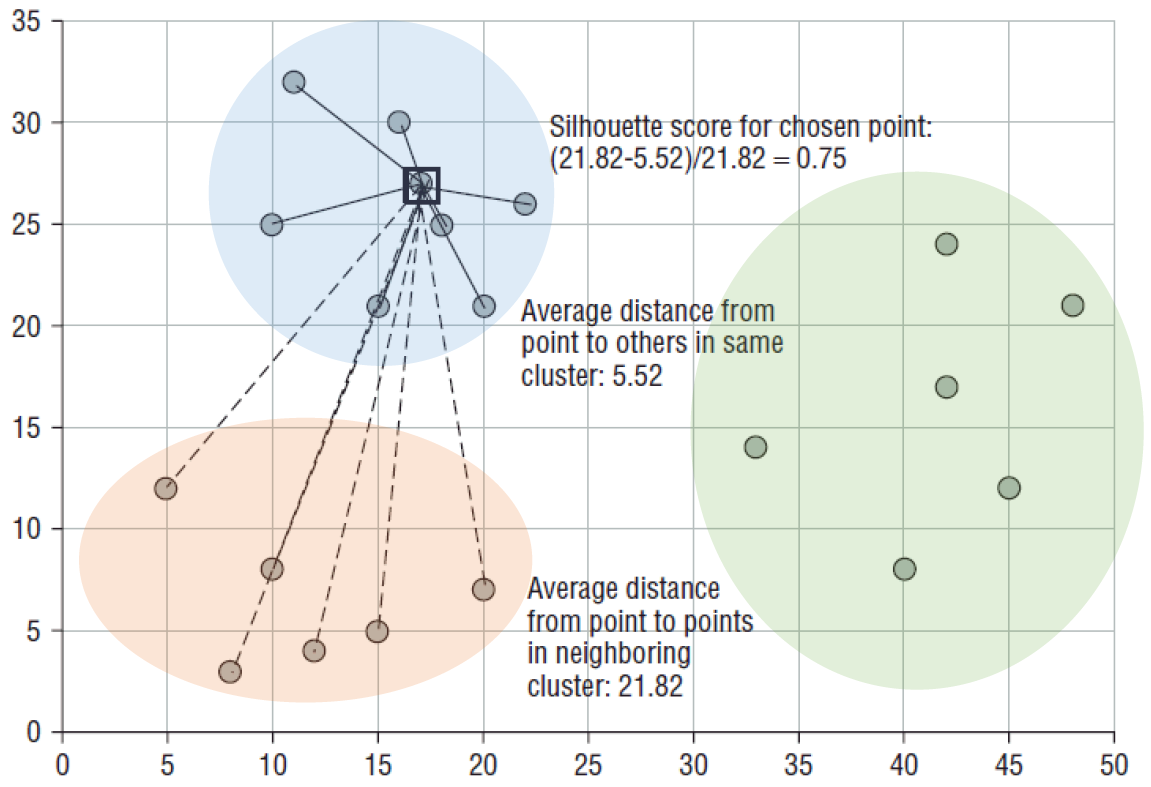
특정 데이터 포인트의 Silhouette Score는
해당 데이터 포인트와 같은 군집 내에 있는 다른 데이터 포인트와의 거리를 평균한 값 a(i),
해당 데이터 포인트가 속하지 않은 군집 중 가장 가까운 군집과의 평균 거리 b(i)를 기반으로 계산된다.
두 군집 간의 거리 값은 b(i) - a(i) 이며 이 값을 정규화 하기 위해 Max(a(i),b(i)) 값으로 나눈다.
이에 따라 -1에서 1의 범위를 가지며, 1에 가까울수록 같은 군집 내의 거리는 최소화되며, 다른 군집간 거리는 최대화됨을 의미한다. 반대로 -1에 가깝게되면 데이터 포인트가 원래 속해야할 군집이 아닌 다른 군집에 속해있음을 의미해 군집화가 적절하지 못하게 진행되었음을 의미한다.
실제로 적용함에 있어서 주의할점은, 비지도학습인 군집분석에서 Silhouette Score는 절대적인 평가지표는 될 수 없다는 것이다. 또한 개별 포인트의 Silhouette Score도 중요하지만, 형성된 군집들간의 계수의 균일성이 더 중요하다고 할 수 있다.
이에따라 K = 3, 4, 5에 따라 형성된 Silhouette Score를 살펴보면 값은 모두 비슷하다. 언급했듯이, 계수의 균일성은 매우 중요한 요소인데 해당 함수에서는 붉은 선위의 군집별 면적이 이를 의미한다. 즉, 붉은 선보다 우측에있는 그래프의 면적이 군집간의 균일할 수록 군집이 타당하게 형성되었다고 볼 수 있다. 이러한 관점에서 K = 3, 4 인 경우가 5일때에 비해서는 적절하게 군집이 형성되었다고 판단했다.
# 군집별 군집의 중심점을 표출
for i in range(3,6):
print("For {} clusters the silhouette score is {:1.2f}".format(i, cluster_centers[i]['silhouette_score']))
print("Centers of each cluster:")
cent_transformed = st.inverse_transform(cluster_centers[i]['cluster_center'])
print(pd.DataFrame(np.exp(cent_transformed),columns=features))
print('-'*50)
rfm['clusters_3'] = cluster_centers[3]['labels']
rfm['clusters_4'] = cluster_centers[4]['labels']
rfm['clusters_5'] = cluster_centers[5]['labels']
fig = plt.figure(figsize=(20,7))
f1 = fig.add_subplot(131)
market = rfm.clusters_3.value_counts()
g = plt.pie(market, labels=market.index, autopct='%.1f%%', shadow=True, startangle=90)
plt.title('3 Clusters')
f1 = fig.add_subplot(132)
market = rfm.clusters_4.value_counts()
g = plt.pie(market, labels=market.index, autopct='%.1f%%', shadow=True, startangle=90)
plt.title('4 Clusters')
f1 = fig.add_subplot(133)
market = rfm.clusters_5.value_counts()
g = plt.pie(market, labels=market.index, autopct='%.1f%%', shadow=True, startangle=90)
plt.title('5 Clusters')
plt.show()
4.3 Cluster Insights
< Recency >
print('Recency In Cluster 3 & 4')
fig = plt.figure(figsize=(20,7))
f1 = fig.add_subplot(121)
sns.boxplot(data=rfm,x='clusters_3',y='Recency')
f1 = fig.add_subplot(122)
sns.boxplot(data=rfm,x='clusters_4',y='Recency')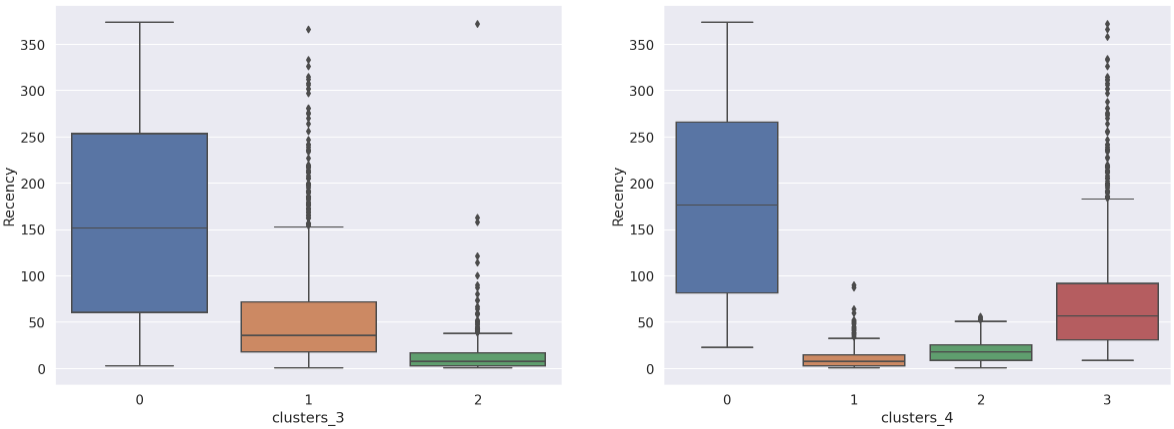
< Frequency >
print('Frequency In Cluster 3 & 4')
fig = plt.figure(figsize=(20,7))
f1 = fig.add_subplot(121)
sns.boxplot(data=rfm,x='clusters_3',y='Frequency')
plt.ylim(0,30)
f1 = fig.add_subplot(122)
sns.boxplot(data=rfm,x='clusters_4',y='Frequency')
plt.ylim(0,30)
< Monetary >
print('Monetary In Cluster 3 & 4')
fig = plt.figure(figsize=(20,7))
f1 = fig.add_subplot(121)
sns.boxplot(data=rfm,x='clusters_3',y='Monetary')
plt.ylim(0,15000)
f1 = fig.add_subplot(122)
sns.boxplot(data=rfm,x='clusters_4',y='Monetary')
plt.ylim(0,15000)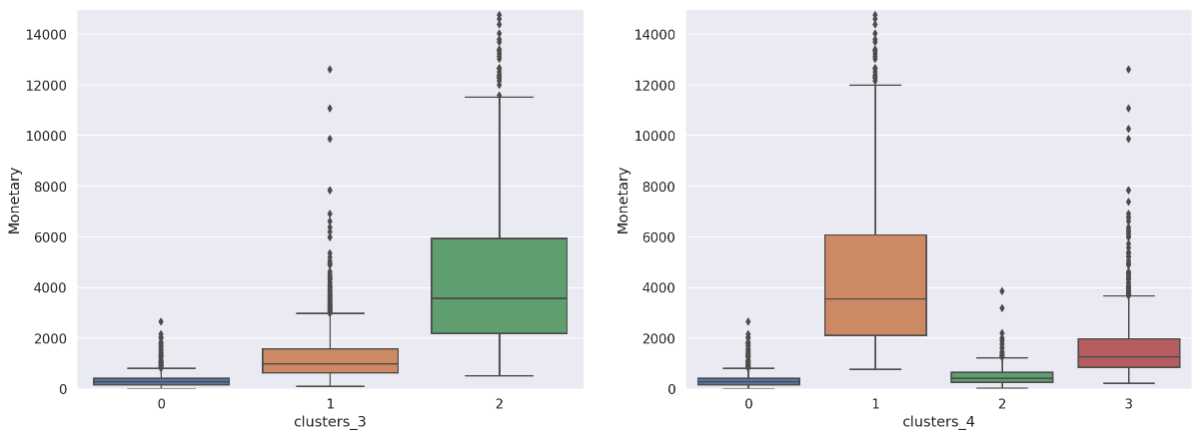
Conclusion
- In the 3-cluster
- 각각의 군집은 R, F, M 면에서 모두 강렬한 차이를 보인다.
- 2번 군집은 Recency는 낮으며 Frequency와 Monetary는 가장 높은 수치를 보여주는 것으로 보아 기업의 수익창출에 있어서 가장 크게 기여하는 집단으로 볼 수있는 열성적인 집단으로 충성 고객 으로 정의할 수 있다.
- 다음으로는 1번 군집, 0번 군집 순으로 이상적인 양상을 보인다.
- 전반적으로 Recency와 Frequency는 Monetary와 pefectly correlate 하고 있다.
(High Monetary-Low Recency-High Frequency).
- In the 4-cluster
- 위의 경우와 달리 Correlate Trend를 따르지 않는 모습이 보인다.
- 3번 군집은 특이하게 2번 군집보다 발생시키는수익이 3배가 넘음에도 불구하고 Recency가 상당히 높다(최근 접근이 오래전이라는 것을 의미한다). 이로보아 3번 군집은 구매 기여도는 상대적으로 높은 수준이나, 최근 구매율이 떨어지는 군집으로 추측된다. 따라서 Target Marketing 을 통해 다시 구매를 유도할 경우 수익증대로 이어질 잠재적 가능성이 높은 군집이다.
- 반대로 2번 군집은 매출 기여도는 낮으나, 상대적으로 Recency 역시 낮아 최근에 구매가 이루어진 집단이다. 즉 최근 구매율은 준수한 편으로 소액의 매출을 발생시키는 군집 또는 신규고객 집단으로 추측된다.
- 0번 군집은 Recency가 타 집단에 비해 상당히 큰 값을 가진다. 극단적인 Recency와 가장 낮은 수준의 Frequency, Monetary는 이탈한 고객들을 대변한다. 해당 군집은 이탈 고객들이 주를 이루는 군집으로 예상된다.
군집의 수가 3일때 보다 4일때 군집이 가지는 고유한 특성이 더 잘 드러나는 양상을 보였다. 3개의 집단에서는 단순히 매출의 기여도에따른 세분화에 주목할 수있었지만, 4개의 집단으로 정의되었을때는 잠재적 고객, 신규고객, 이탈고객 양상 등의 구체적인 행동 패턴이 유추될 수 있었다. 실루엣 계수는 3개의 군집일때가 더 높았으나, 실제 해석과 Insight 창출 및 적용에 있어서 4개의 군집으로 정의하는 것이 더 이상적으로 보인다. 이는 곧 집단별 차별화된 마케팅 전략의 수립, 고객 행동양상 정의 등의 새로운 제안이나 분석으로 이어질 수 있으며 기업차원의 가치창출과 수익창출의 극대화로 직결될 수 있다.